Кога станува збор заантени, прашањето за кое луѓето најмногу се грижат е „Како всушност се постигнува зрачењето?“ Како електромагнетното поле генерирано од изворот на сигнал се шири низ далноводот и во внатрешноста на антената, и конечно се „одвојува“ од антената за да формира бран во слободен простор.
1. Едножично зрачење
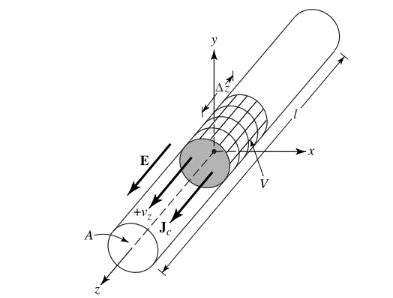
Да претпоставиме дека густината на полнежот, изразена како qv (Кулон/m3), е рамномерно распределена во кружна жица со пресек од a и волумен од V, како што е прикажано на Слика 1.
Слика 1
Вкупниот полнеж Q во волуменот V се движи во насока z со рамномерна брзина Vz (m/s). Може да се докаже дека густината на струјата Jz на пресекот на жицата е:
Jz = qv vz (1)
Ако жицата е направена од идеален спроводник, густината на струјата Js на површината на жицата е:
Js = qs vz (2)
Каде што qs е густината на површинскиот полнеж. Ако жицата е многу тенка (идеално, радиусот е 0), струјата во жицата може да се изрази како:
Iz = ql vz (3)
Каде што ql (кулон/метар) е полнежот по единица должина.
Главно се занимаваме со тенки жици, а заклучоците се однесуваат на горенаведените три случаи. Ако струјата е временски променлива, изводот на формулата (3) во однос на времето е како што следува:
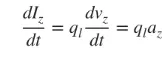
(4)
az е забрзувањето на полнежот. Ако должината на жицата е l, (4) може да се запише на следниов начин:
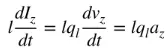
(5)
Равенката (5) е основната врска помеѓу струјата и полнежот, а исто така и основната врска на електромагнетното зрачење. Едноставно кажано, за да се произведе зрачење, мора да постои временски променлива струја или забрзување (или забавување) на полнежот. Обично ја споменуваме струјата во временски хармонични апликации, а полнежот најчесто се споменува во преодни апликации. За да се произведе забрзување (или забавување) на полнежот, жицата мора да биде свиткана, превиткана и дисконтинуирана. Кога полнежот осцилира во временски хармонично движење, тој исто така ќе произведе периодично забрзување (или забавување) на полнежот или временски променлива струја. Затоа:
1) Ако полнежот не се помести, нема да има струја и нема да има зрачење.
2) Ако полнежот се движи со константна брзина:
а. Ако жицата е права и бесконечна по должина, нема зрачење.
б. Ако жицата е свиткана, превиткана или дисконтинуирана, како што е прикажано на Слика 2, постои зрачење.
3) Ако полнежот осцилира со текот на времето, полнежот ќе зрачи дури и ако жицата е права.
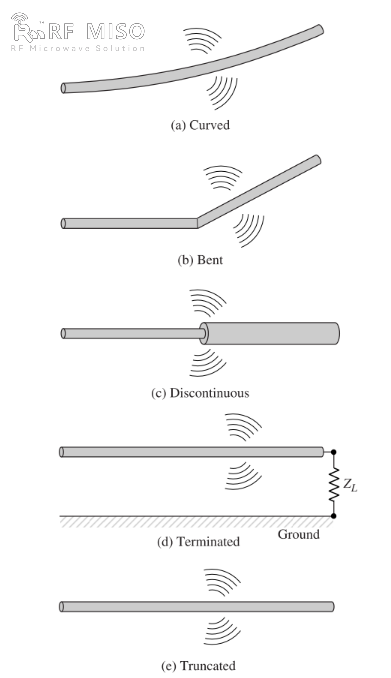
Слика 2
Квалитативно разбирање на механизмот на зрачење може да се добие со разгледување на пулсен извор поврзан со отворена жица што може да се заземји преку оптоварување на нејзиниот отворен крај, како што е прикажано на Слика 2(d). Кога жицата првично е напојувана, полнежите (слободните електрони) во жицата се ставаат во движење од линиите на електричното поле генерирани од изворот. Како што полнежите се забрзуваат на изворниот крај на жицата и се забавуваат (негативно забрзување во однос на првичното движење) кога се рефлектираат на нејзиниот крај, поле на зрачење се генерира на неговите краеви и по должината на остатокот од жицата. Забрзувањето на полнежите се постигнува со надворешен извор на сила што ги става полнежите во движење и го произведува поврзаното поле на зрачење. Забавувањето на полнежите на краевите на жицата се постигнува со внатрешни сили поврзани со индуцираното поле, кое е предизвикано од акумулацијата на концентрирани полнежи на краевите на жицата. Внатрешните сили добиваат енергија од акумулацијата на полнежот како што неговата брзина се намалува на нула на краевите на жицата. Затоа, забрзувањето на полнежите поради возбудата од електричното поле и забавувањето на полнежите поради дисконтинуитетот или мазната крива на импедансата на жицата се механизмите за генерирање на електромагнетно зрачење. Иако и густината на струјата (Jc) и густината на полнежот (qv) се изворни термини во Максвеловите равенки, полнежот се смета за пофундаментална величина, особено за минливи полиња. Иако ова објаснување за зрачењето главно се користи за минливи состојби, може да се користи и за објаснување на зрачењето во стационарна состојба.
Препорачајте неколку одличниантенски производипроизведено одРФМИСО:
2. Двожично зрачење
Поврзете извор на напон на двожичен далновод поврзан со антена, како што е прикажано на Слика 3(а). Применувањето на напон на двожичната линија генерира електрично поле помеѓу спроводниците. Линиите на електричното поле дејствуваат на слободните електрони (лесно одвоени од атомите) поврзани со секој спроводник и ги принудуваат да се движат. Движењето на полнежите генерира струја, која пак генерира магнетно поле.
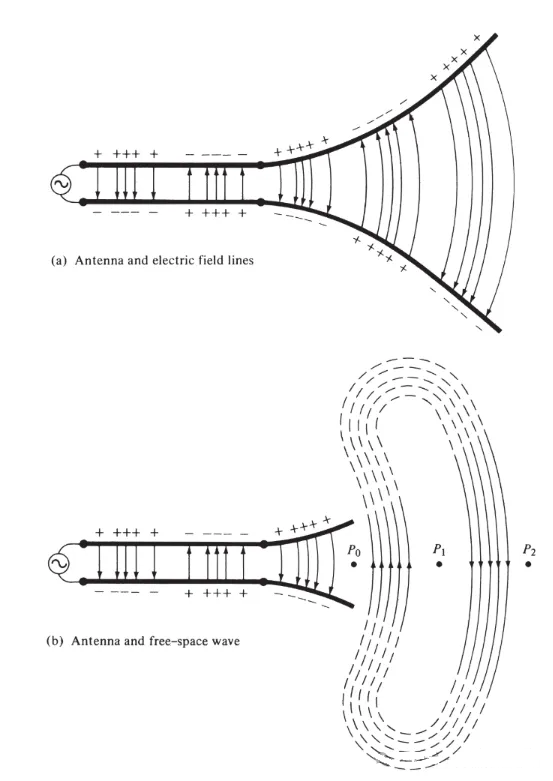
Слика 3
Прифативме дека линиите на електричното поле почнуваат со позитивни полнежи и завршуваат со негативни полнежи. Секако, тие можат да почнуваат и со позитивни полнежи и да завршуваат во бесконечност; или да почнуваат во бесконечност и да завршуваат со негативни полнежи; или да формираат затворени јамки кои ниту почнуваат ниту завршуваат со полнежи. Линиите на магнетното поле секогаш формираат затворени јамки околу спроводници што носат струја, бидејќи во физиката нема магнетни полнежи. Во некои математички формули, се воведуваат еквивалентни магнетни полнежи и магнетни струи за да се покаже двојноста помеѓу решенијата што вклучуваат моќност и магнетни извори.
Линиите на електричното поле нацртани помеѓу два спроводници помагаат да се прикаже распределбата на полнежот. Ако претпоставиме дека изворот на напон е синусоиден, очекуваме електричното поле помеѓу спроводниците исто така да биде синусоидно со период еднаков на оној на изворот. Релативната големина на јачината на електричното поле е претставена со густината на линиите на електричното поле, а стрелките ја означуваат релативната насока (позитивна или негативна). Генерирањето на временски променливи електрични и магнетни полиња помеѓу спроводниците формира електромагнетен бран што се шири по должината на преносната линија, како што е прикажано на Слика 3(а). Електромагнетниот бран влегува во антената со полнежот и соодветната струја. Ако отстраниме дел од структурата на антената, како што е прикажано на Слика 3(б), може да се формира бран на слободен простор со „поврзување“ на отворените краеви на линиите на електричното поле (прикажани со испрекинатите линии). Бранот на слободен простор е исто така периодичен, но точката со константна фаза P0 се движи нанадвор со брзината на светлината и патува растојание од λ/2 (до P1) за половина временски период. Во близина на антената, точката со константна фаза P0 се движи побрзо од брзината на светлината и се приближува до брзината на светлината во точките што се далеку од антената. Слика 4 ја прикажува распределбата на електричното поле во слободниот простор на антената λ∕2 при t = 0, t/8, t/4 и 3T/8.
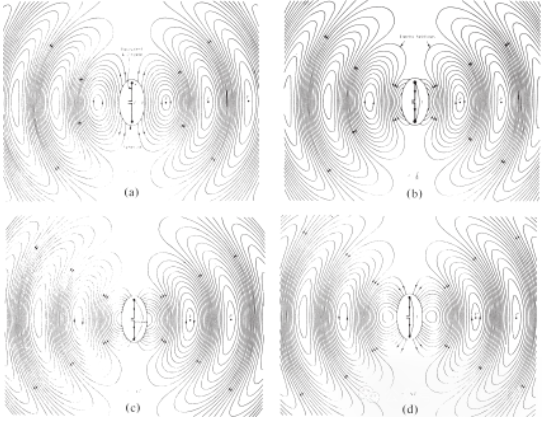
Слика 4 Распределба на електричното поле во слободен простор на антената λ∕2 при t = 0, t/8, t/4 и 3T/8
Не е познато како водените бранови се одделуваат од антената и на крајот се формираат за да се шират во слободен простор. Можеме да ги споредиме водените бранови и брановите во слободен простор со водните бранови, кои можат да бидат предизвикани од камен фрлен во мирна површина на вода или на други начини. Откако ќе започне нарушувањето во водата, се генерираат водни бранови и почнуваат да се шират нанадвор. Дури и ако нарушувањето престане, брановите не запираат, туку продолжуваат да се шират напред. Ако нарушувањето продолжи, постојано се генерираат нови бранови, а ширењето на овие бранови заостанува зад другите бранови.
Истото важи и за електромагнетните бранови генерирани од електрични пречки. Ако почетното електрично пречки од изворот е краткотрајно, генерираните електромагнетни бранови се шират во далноводот, потоа влегуваат во антената и конечно зрачат како бранови во слободен простор, иако возбудата повеќе не е присутна (исто како водените бранови и пречките што ги создаваат). Ако електричното пречки е континуирано, електромагнетните бранови постојат континуирано и ги следат внимателно за време на ширењето, како што е прикажано на биконусната антена прикажана на Слика 5. Кога електромагнетните бранови се во далноводите и антените, нивното постоење е поврзано со постоењето на електричен полнеж во проводникот. Меѓутоа, кога брановите се зрачат, тие формираат затворена јамка и нема полнеж за да го одржат своето постоење. Ова нè води до заклучокот дека:
Побудувањето на полето бара забрзување и забавување на полнежот, но одржувањето на полето не бара забрзување и забавување на полнежот.
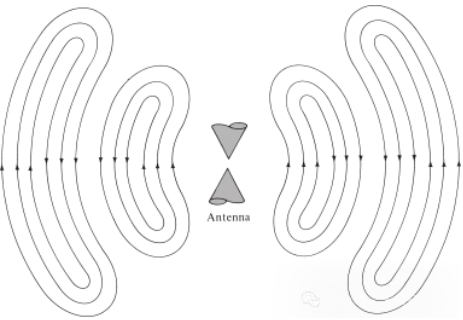
Слика 5
3. Диполско зрачење
Се обидуваме да го објасниме механизмот со кој линиите на електричното поле се одвојуваат од антената и формираат бранови на слободен простор, и ја земаме диполната антена како пример. Иако е поедноставено објаснување, тоа исто така им овозможува на луѓето интуитивно да го видат генерирањето на бранови на слободен простор. Слика 6(а) ги прикажува линиите на електричното поле генерирани помеѓу двата крака на диполот кога линиите на електричното поле се движат нанадвор за λ∕4 во првата четвртина од циклусот. За овој пример, да претпоставиме дека бројот на формирани линии на електричното поле е 3. Во следната четвртина од циклусот, оригиналните три линии на електричното поле се поместуваат за уште λ∕4 (вкупно λ∕2 од почетната точка), а густината на полнежот на проводникот почнува да се намалува. Може да се смета дека е формирана со воведување на спротивни полнежи, кои ги поништуваат полнежите на проводникот на крајот од првата половина од циклусот. Линиите на електричното поле генерирани од спротивните полнежи се 3 и се движат на растојание од λ∕4, што е претставено со испрекинатите линии на Слика 6(б).
Конечниот резултат е дека постојат три линии на електричното поле насочени надолу на првото λ∕4 растојание и ист број на линии на електричното поле насочени нагоре на второто λ∕4 растојание. Бидејќи нема нето полнеж на антената, линиите на електричното поле мора да бидат принудени да се одвојат од проводникот и да се спојат за да формираат затворена јамка. Ова е прикажано на Слика 6(c). Во втората половина, се следи истиот физички процес, но имајте предвид дека насоката е спротивна. После тоа, процесот се повторува и продолжува бесконечно, формирајќи распределба на електричното поле слична на Слика 4.
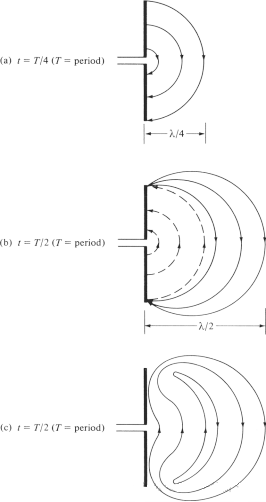
Слика 6
За да дознаете повеќе за антените, посетете ја страницата:
Време на објавување: 20 јуни 2024 година










